一些出现在我的草稿本上的奇怪的题目。
Problem 1
\[\begin{align} &证明\sum_{i=0}^{n}C_{2n}^{2n-i}C_{2n-i}^{i}2^{2n-2i}=C_{4n}^{2n}.\\ &\large{咕咕咕}. \end{align}\]Problem 2
\[\begin{align} &一三角形三边长为\sqrt{445},\sqrt{808},\sqrt{1017},求这个三角形的面积.\\ &\textbf{解法1:}设AB=\sqrt{808},BC=\sqrt{1417},AC=\sqrt{445}.\\ &作AB边上的高CM,垂足为M,设CM=h,AM=a.\\ &由图,使用两次勾股定理,可得h^2=\sqrt{445}^2-a^2=\sqrt{1417}^2-(a+\sqrt{808})^2\\ &解得h=\frac{297\sqrt{202}}{202}.\\ &三角形面积S=\frac{1}{2}AB\cdot h=297.\\ &\textbf{解法2:}\cos B=\frac{AB^2+BC^2-AC^2}{2AB\cdot BC}=\frac{1780}{2\sqrt{808\times 1017}}.\\ &设x=\sqrt{808\times 1017},则\cos B=\frac{1780}{2x}=\frac{890}{x}.\\ &则\sin B=\sqrt{1-\cos^2 B}=\sqrt{\frac{x^2-890^2}{x^2}}.\\ &则S=\frac{1}{2}AB\cdot BC\sin B\\ &=\frac{1}{2}\sqrt{808}\sqrt{1017}\sqrt{\frac{x^2-890^2}{x^2}}\\ &=\frac{1}{2}x\sqrt{\frac{808\times 1017-890^2}{x^2}}\\ &=\sqrt{88209}\\ &=297.\\ \\ \\ &题外话:这题出自某次南外数学提高班选拔.\\ \end{align}\]Problem 3
\[\begin{align} &经典题:\{a_n\}是公差为d的等差数列,\{b_n\}是公比为q的等比数列,求T_n=\sum_{i=1}^na_ib_i.\\ &\textbf{解:}T_n=a_1b_1+a_2b_2+a_3b_3+\cdots+a_nb_n\qquad\qquad(1)\\ &qT_n=a_1b_2+a_2b_3+a_3b_4+\cdots+a_nb_{n+1}\qquad\qquad(2)\\ &\therefore(1-q)T_n=a_1b_1+d(b_2+b_3+\cdots+b_n)-a_nb_{n+1}\\ &=a_1b_1+d\cdot\frac{b_2(1-q^{n-1})}{1-q}-[a_1+(n-1)d]b_1q^n.\\ &\therefore T_n=\frac{a_1b_1(1-q)+dqb_1(1-q^{n-1})-[a_1+(n-1)d]b_1q^n}{(1-q)^2}.\\ &\\ &题外话:这题约等于\text{2025}年全国卷\text{I}数列原题.\\ \end{align}\]Problem 4
\[\begin{align} &找到最小的正整数q,使得存在正整数p,满足\frac{p}{q}=0.2025\cdots(即[\frac{10000p}{q}]=2025)且p,q互质.\\ &\textbf{解:}\frac{81}{400}=0.2025显然,下讨论q<400情况:\\ &由题,2025<\frac{10000p}{q}<2026,即2025q<10000p<2026q.\\ &由于q<400,故[\frac{q}{5}]\times 10000<2025q<([\frac{q}{5}]+1)\times 10000,\\ &要使2025q<10000p<2026q,就要使2026q>([\frac{q}{5}]+1)\times 10000.\\ &设q=5k+r(k\in \mathbb{N},r=0,1,2,3,4)\\ &则2026(5k+r)>(k+1)\times 10000,可得k>\frac{10000-2026r}{130}\\ &引理:若a=k_1+r_1,b=k_2+r_2,k_1<k_2,则a<b.\\ &证明:k_1\le k_2-1,r_1\le 4,r_2\ge0,则a_{max}=5(k_2-1)+4,b_{min}=5k_2,易得b_{min}>a_{max}\\ &所以有a<b.\\ &由引理知,要使q最小,就要使k最小,\\ &当r=4时,k取最小值k_{min}=15,\\ &此时q_{min}=5k_{min}+r=79.\\ &综上,满足条件的最小的q为79.\\ \\ \\ &题外话:这题是南师附中\text{2025}特长生真题.\\ \end{align}\]Problem 5
\[\begin{align} &若\sum x_i=1,证明\sum\sqrt{x_i}\cdot\sum\frac{1}{\sqrt{x_i+1}}\le\frac{n^2}{\sqrt{n+1}}.\\ &\textbf{证明:}令s=\sum\sqrt{x_i},\\ &则s=\sum\sqrt{x_i}=\sum 1\cdot\sqrt{x_i}\le\sqrt{\sum 1^2\cdot\sum\sqrt{x_i}^2}=\sqrt{n}.\\ &令t=\sum\sqrt{x_i+1},\\ &\because\sum\frac{1}{\sqrt{x_i+1}}=\sum\frac{1+x_i-x_i}{\sqrt{x_i+1}}=\sum\sqrt{x_i+1}-\sum\frac{x_i}{\sqrt{x_i+1}}=t-\sum\frac{x_i}{\sqrt{x_i+1}}\\ &且\sum\frac{x_i}{\sqrt{x_i+1}}\cdot\sum{\sqrt{x_i+1}}\ge(\sum\sqrt{x_i})^2=s^2,\\ &\therefore\sum\frac{1}{\sqrt{x_i+1}}=t-\sum\frac{x_i}{\sqrt{x_i+1}}\le t-\frac{s^2}{\sum\sqrt{x_i+1}}=t-\frac{s^2}{t}.\\ &欲证命题化为s(t-\frac{s^2}{t})\le\frac{n^2}{\sqrt{n+1}}.\\ &又由于t=\sum\sqrt{x_i+1}=\sum 1\cdot\sqrt{x_i+1}\le \sqrt{\sum 1^2\cdot \sum(x_i+1)}=\sqrt{n(n+1)}\\ &且t-\frac{s^2}{t}是t的增函数\\ &故有s(t-\frac{s^2}{t})\le s[\sqrt{n(n+1)}-\frac{s^2}{\sqrt{n(n+1)}}]=\frac{n(n+1)s-s^3}{\sqrt{n(n+1)}}.\\ &当n=1时,原不等式显然成立;\\ &n\ge 2时,令f(s)=n(n+1)s-s^3\\ &当s\le\sqrt{n}时,f'(s)=n(n+1)-3s^2\ge n(n+1)-3n=n(n-2)\ge 0\\ &即f(s)在s\le \sqrt{n}时递增,即f(s)_{max}=f(\sqrt{n})\\ &故s(t-\frac{s^2}{t})\le\frac{n(n+1)s-s^3}{\sqrt{n(n+1)}}\le\frac{n(n+1)\sqrt{n}-(\sqrt{n}^3)}{\sqrt{n(n+1)}}=\frac{n^2}{\sqrt{n+1}}.即原命题得证.\\ \\ \\ &题外话:在单墫老师的书上看到的题目,条件很严格,证明也很富有技巧性,尤其需要对柯西不等式的熟练掌握.\\ \end{align}\]Problem 6
\[如图,AB=BC=CD,\angle ABC=100^{\circ},\angle BCD=20^{\circ},求\angle BAD的大小.\]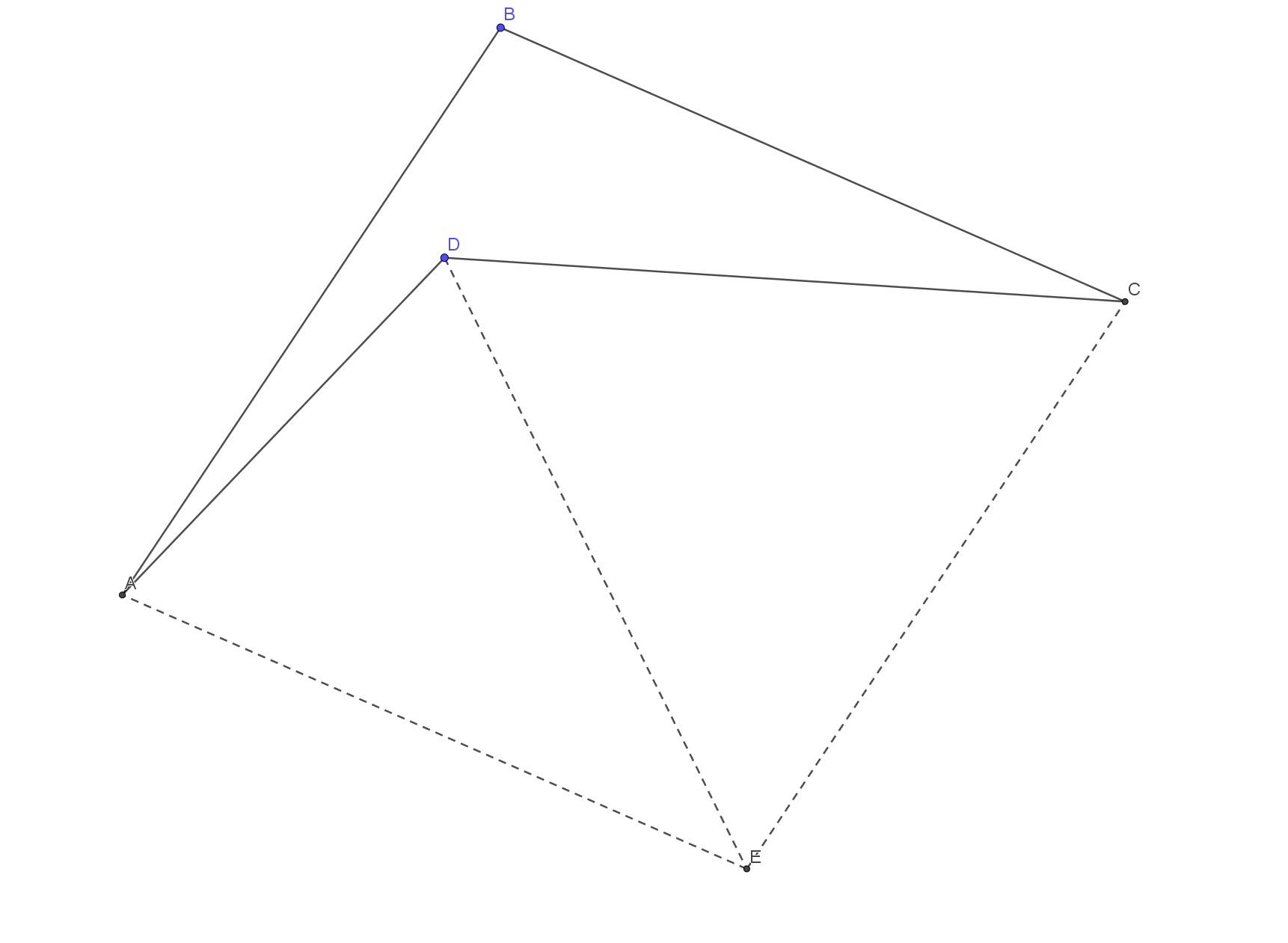 \(\begin{align}
&以CD为一条边,向左下作等边三角形CDE.\\
&由题,AB=BC=CD=DE=CE,\\
&\angle BCE=\angle BCD+\angle DCE=20^{\circ}+60^{\circ}=80^{\circ}.\\
&\therefore\angle B+\angle BCE=100^{\circ}+80^{\circ}=180^\circ\\
&\therefore AB//CE\\
&又\because AB=CE\\
&\therefore 四边形ABCE是平行四边形,又\because AB=BC\\
&\therefore 平行四边形ABCE是菱形\\
&导角即可得到\angle BAD=10^\circ.\\
\\
&题外话:神秘的辅助线.之前好像还用圆证了一遍,但现在忘了.\\
\end{align}\)
\(\begin{align}
&以CD为一条边,向左下作等边三角形CDE.\\
&由题,AB=BC=CD=DE=CE,\\
&\angle BCE=\angle BCD+\angle DCE=20^{\circ}+60^{\circ}=80^{\circ}.\\
&\therefore\angle B+\angle BCE=100^{\circ}+80^{\circ}=180^\circ\\
&\therefore AB//CE\\
&又\because AB=CE\\
&\therefore 四边形ABCE是平行四边形,又\because AB=BC\\
&\therefore 平行四边形ABCE是菱形\\
&导角即可得到\angle BAD=10^\circ.\\
\\
&题外话:神秘的辅助线.之前好像还用圆证了一遍,但现在忘了.\\
\end{align}\)