并查集判环是个好东西,代码很短,但我赛时脑抽没想出来。
分析
首先,如果能回到起点,那么肯定是走了一个环。
这是一个什么样的环呢?
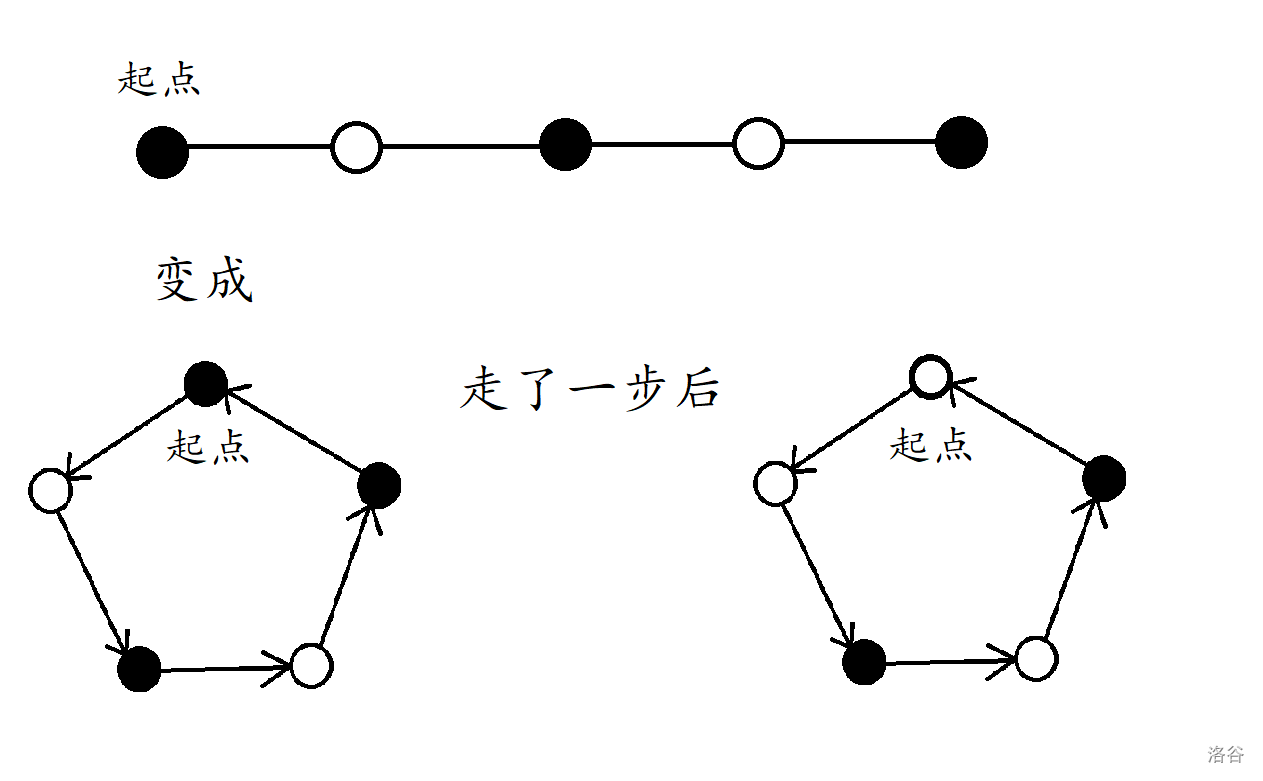
我们设起点的颜色为黑色,那么下一个点的颜色一定和起点不一样,这样才能走到下一个点,所以下一个点的颜色是白色。那再下面一个点的颜色又是黑色了,以此类推。
那我们在外面兜兜转转了一圈,终究是要走回起点的。当你的下一步要走回起点时,起点的颜色已经被反转了,也就是说,此时起点的颜色是白色。那么,走向起点的这个点一定是黑色的,这样才能走回起点。
如果起点是白色的,那么同理,下一个点是黑色,再下一个点是白色……最后走向起点的这个点是白色的,最后走回起点。
所以,我们要找由一条黑白相间,两端颜色一致的链拼起来的一个环。
可以配合下图食用:
那就可以用并查集维护。
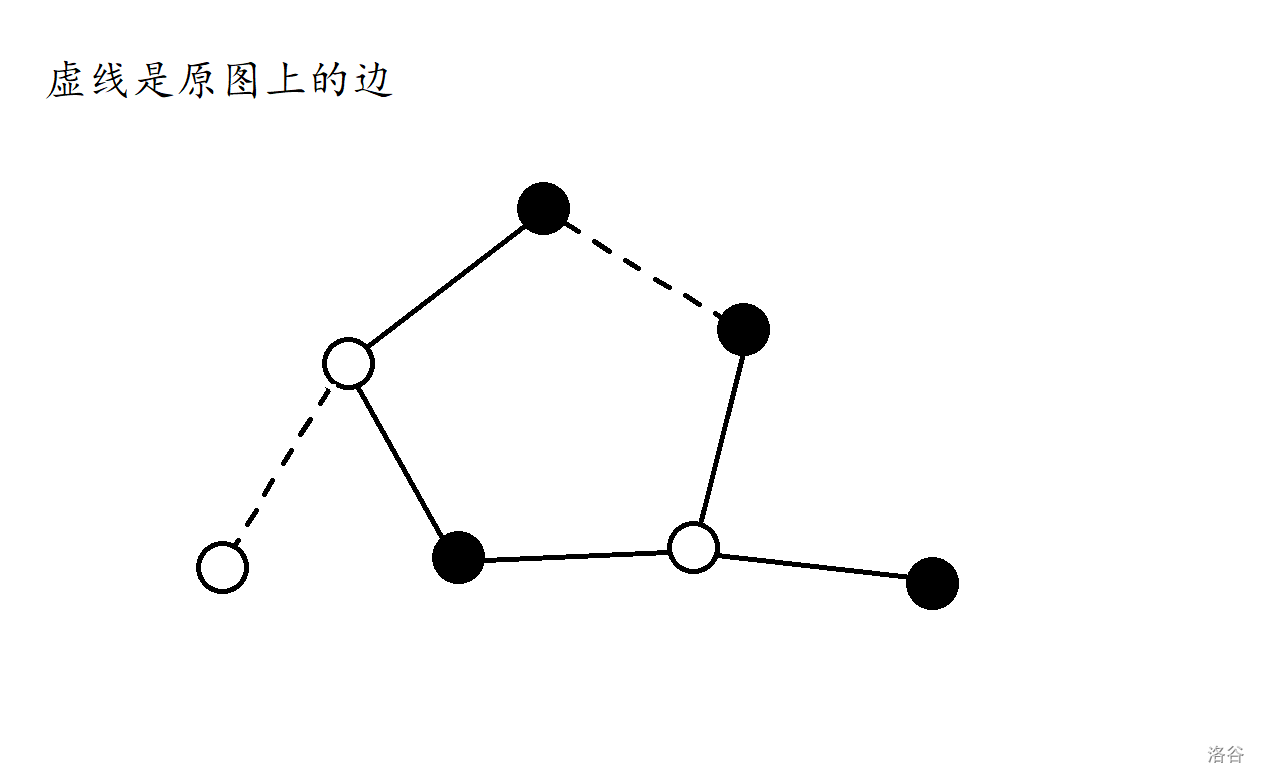
step1.把所有不同颜色的相邻的点在并查集中连边
如下图,这样就满足了黑白相间的要求。
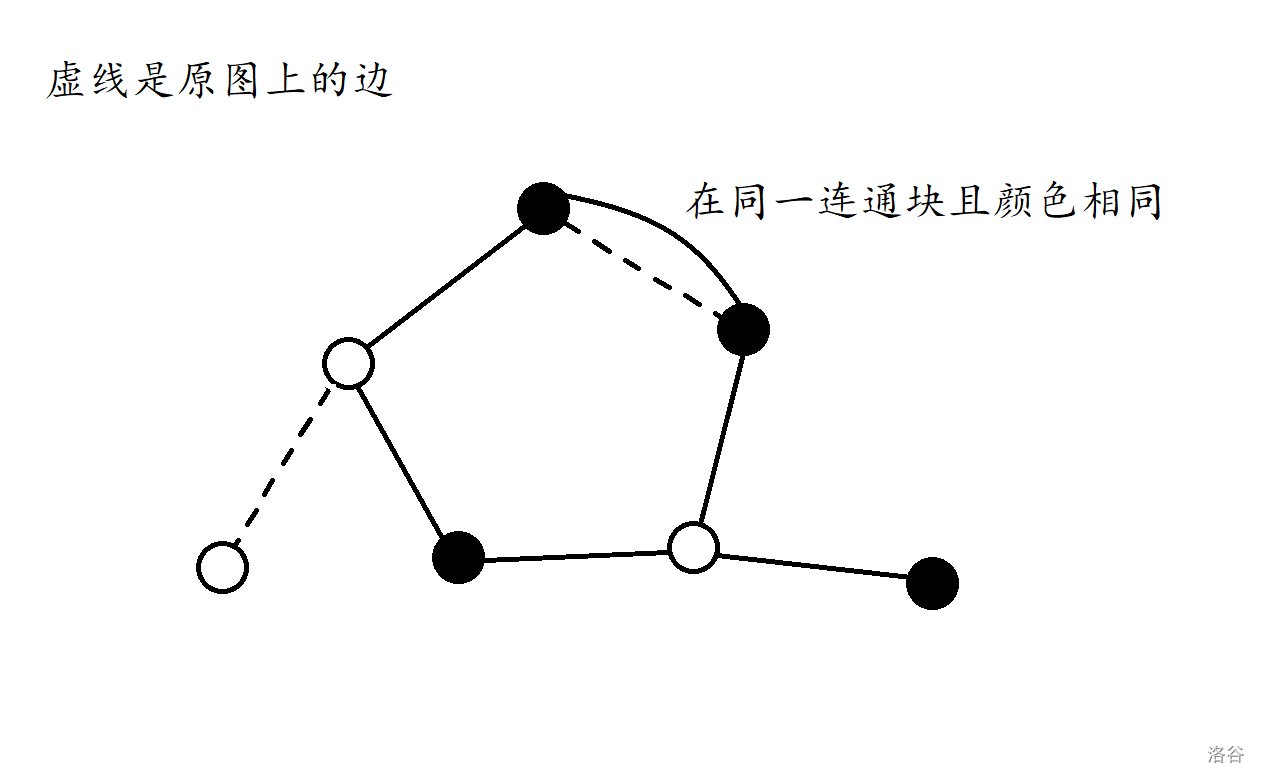
step2.查询是否有相邻的,颜色一致且在同一连通块的两个点
如果有,就满足了两端颜色一致的要求。见下图。
代码如下:
#include <bits/stdc++.h>
using namespace std;
struct edge { int u, v; } e[200005];
int n, m, fa[200005], c[200005];
bool ok;
//并查集基本操作
int find(int x) { return x == fa[x] ? x : fa[x] = find(fa[x]); }
void merge(int x, int y) { fa[find(x)] = find(y); }
int main() {
cin >> n >> m;
for(int i = 1; i <= m; i++) {
int u, v;
cin >> u >> v;
e[i] = (edge){u, v};
}
for(int i = 1; i <= n; i++) cin >> c[i];
for(int i = 1; i <= n; i++) fa[i] = i; //并查集初始化
for(int i = 1; i <= m; i++) if (c[e[i].u] != c[e[i].v]) merge(e[i].u, e[i].v); //如果两个点相邻且不同色,连边
for(int i = 1; i <= m; i++) if (c[e[i].u] == c[e[i].v] && find(e[i].u) == find(e[i].v)) ok = 1; //查询是否有相邻的,颜色一致且在同一连通块的两个点
if (ok) puts("Yes");
else puts("No");
return 0;
}